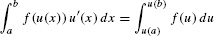5.6 Substitution Method
Integration (antidifferentiation) is generally more difficult than differentiation. There are no sure-fire methods, and many antiderivatives cannot be expressed in terms of elementary functions. However, there are a few important general techniques. One such technique is the Substitution Method, which uses the Chain Rule “in reverse.”
The term “integration” is used in two ways. It refers to:
- The process of finding signed area (computing a definite integral), and also
- The process of finding an antiderivative (evaluating an indefinite integral).
Consider the integral 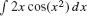 . We can evaluate it if we remember the Chain Rule calculation
. We can evaluate it if we remember the Chain Rule calculation
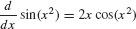
This tells us that sin(x2) is an antiderivative of 2x cos(x2), and therefore,

A similar Chain Rule calculation shows that
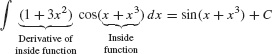
In both cases, the integrand is the product of a composite function and the derivative of the inside function. The Chain Rule does not help if the derivative of the inside function is missing. For instance, we cannot use the Chain Rule to compute 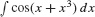 because the factor (1 + 3x2) does not appear.
because the factor (1 + 3x2) does not appear.
 REMINDER A “composite function” is a function of the form f(g(x)). For convenience, we call g(x) the inside function and f(u) the outside function.
REMINDER A “composite function” is a function of the form f(g(x)). For convenience, we call g(x) the inside function and f(u) the outside function.
329
In general, if F′(u) = f(u), then by the Chain Rule,
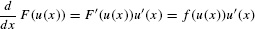
This translates into the following integration formula:
THEOREM 1 The Substitution Method
If F′(x) = f(x), then
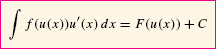
Substitution Using Differentials
Before proceeding to the examples, we discuss the procedure for carrying out substitution using differentials. Differentials are symbols such as du or dx that occur in the Leibniz notations du/dx and 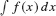 . In our calculations, we shall manipulate them as though they are related by an equation in which the dx “cancels”:
. In our calculations, we shall manipulate them as though they are related by an equation in which the dx “cancels”:
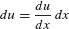
Equivalently, du and dx are related by

For example,

Now when the integrand has the form f(u(x)) u′(x), we can use Eq. (1) to rewrite the entire integral (including the dx term) in terms of u and its differential du:
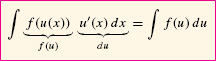
The symbolic calculus of substitution using differentials was invented by Leibniz and is considered one of his most important achievements. It reduces the otherwise complicated process of transforming integrals to a convenient set of rules.
This equation is called the Change of Variables Formula. It transforms an integral in the variable x into a (hopefully simpler) integral in the new variable u.
EXAMPLE 1
Evaluate 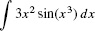 .
.
Solution The integrand contains the composite function sin(x3), so we set u = x3. The differential du = 3x2 dx also appears, so we can carry out the substitution:
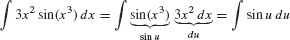
In substitution, the key step is to choose the appropriate inside function u.
Now evaluate the integral in the u-variable and replace u by x3 in the answer:
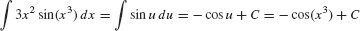
330
Let’s check our answer by differentiating:
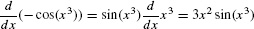
EXAMPLE 2 Multiplying [em]du[/em] by a Constant
Evaluate 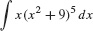 .
.
Solution We let u = x2 + 9 because the composite u5 = (x2 + 9)5 appears in the integrand. The differential du = 2x dx does not appear as is, but we can multiply by  to obtain
to obtain
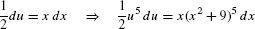
Now we can apply substitution:
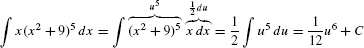
Finally, we express the answer in terms of x by substituting u = x2 + 9:
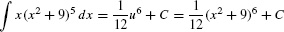
Substitution Method:
- (1) Choose u and compute du.
- (2) Rewrite the integral in terms of u and du, and evaluate.
- (3) Express the final answer in terms of x.
EXAMPLE 3
Evaluate 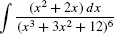 .
.
Solution The appearance of (x3 + 3x2 + 12)−6 in the integrand suggests that we try u = x3 + 3x2 + 12. With this choice,
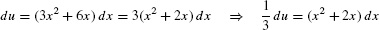
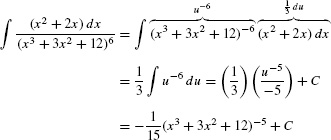
CONCEPTUAL INSIGHT
An integration method that works for a given function may fail if we change the function even slightly. In the previous example, if we replace 2 by 2.1 and consider instead 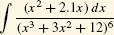 , the Substitution Method does not work. The problem is that (x2 + 2.1x) dx is not a multiple of du = (3x2 + 6x) dx.
, the Substitution Method does not work. The problem is that (x2 + 2.1x) dx is not a multiple of du = (3x2 + 6x) dx.
EXAMPLE 4
Evaluate 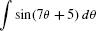 .
.
Solution Let u = 7θ + 5. Then du = 7dθ and 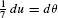 . We obtain
. We obtain
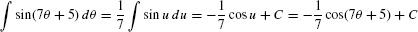
331
EXAMPLE 5
Evaluate 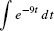 .
.
Solution Use the substitution u = −9t, du = −9 dt:
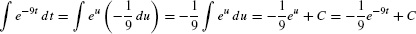
EXAMPLE 6
Evaluate 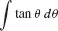 .
.
Solution In this case, the idea is to write 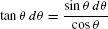 and to note that if u = cos θ. Then du = −sin θ dθ and
and to note that if u = cos θ. Then du = −sin θ dθ and
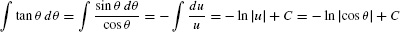
Now recall that 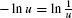 . Thus,
. Thus, 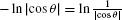 , and we obtain
, and we obtain
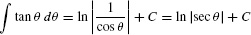
The substitution method does not always work, even when the integral looks relatively simple. For example, 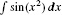 cannot be evaluated explicitly by substitution, or any other method. With experience, you will learn to recognize when substitution is likely to be successful.
cannot be evaluated explicitly by substitution, or any other method. With experience, you will learn to recognize when substitution is likely to be successful.
EXAMPLE 7 Additional Step Necessary
Evaluate 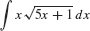 .
.
Solution Since 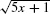 appears, we are tempted to set u = 5x + 1. Then
appears, we are tempted to set u = 5x + 1. Then
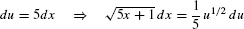
Unfortunately, the integrand is not 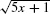 but
but 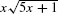 . To take care of the extra factor of x, we solve u = 5x + 1 to obtain
. To take care of the extra factor of x, we solve u = 5x + 1 to obtain 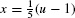 . Then
. Then
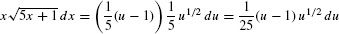
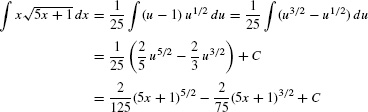
Change of Variables Formula for Definite Integrals
The Change of Variables Formula can be applied to definite integrals provided that the limits of integration are changed, as indicated in the next theorem.
Change of Variables Formula for Definite Integrals
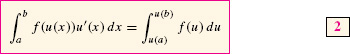
The new limits of integration with respect to the u-variable are u(a) and u(b). Think of it this way: As x varies from a to b, the variable u = u(x) varies from u(a) to u(b).
332
Proof
If F(x) is an antiderivative of f(x), then F(u(x)) is an antiderivative of f(u(x))u′(x). FTC I shows that the two integrals are equal:
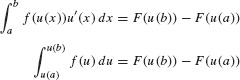
Change of Variables for definite integrals:
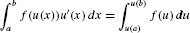
EXAMPLE 8
Evaluate 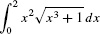 .
.
Solution Use the substitution u = x3 + 1, du = 3x2 dx:
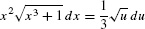
By Eq. (2), the new limits of integration
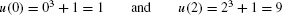
Thus,
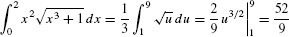
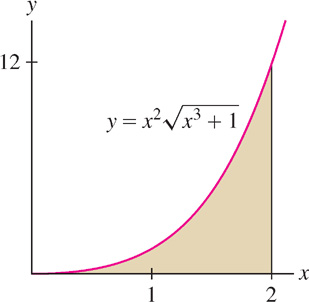
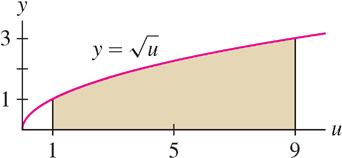
This substitution shows that the area in Figure 1 is equal to one-third of the area in Figure 2 (but note that the figures are drawn to different scales).
 .
.
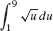 .
.
In the previous example, we can avoid changing the limits of integration by evaluating the integral in terms of x.
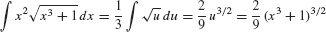
This leads to the same result: 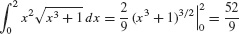 .
.
EXAMPLE 9
Evaluate 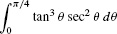 .
.
Solution The substitution u = tan θ makes sense because du = sec2 θ dθ and therefore, u3 du = tan3 θ sec2 θ dθ. The new limits of integration are
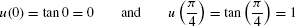
Thus,
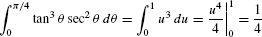
EXAMPLE 10
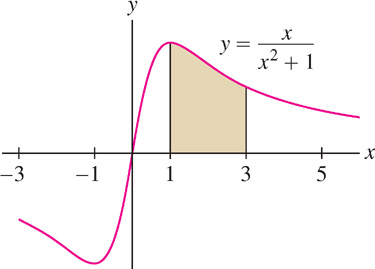
Calculate the area under the graph of 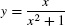 over [1, 3].
over [1, 3].
Solution The area (Figure 3) is equal to 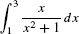 . We use the substitution
. We use the substitution
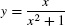 over [1, 3].
over [1, 3].
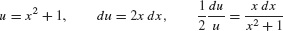
333
The new limits of integration are u(1) = 12 + 1 = 2 and u(3) = 32 + 1 = 10, so
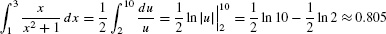
5.6.1 Summary
- Try the Substitution Method when the integrand has the form f(u(x)) u′(x). If F is an antiderivative of f, then
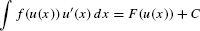
- The differential of u(x) is related to dx by du = u′(x) dx.
- The Substitution Method is expressed by the Change of Variables Formula:
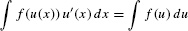
- Change of Variables Formula for definite integrals: